| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 18405
- 14620
- 7785
- 18352
- 컨텐츠 기반 필터링
- 넷플릭스 추천 시스템
- 앤드류 응
- 알고리즘
- 문자열반전
- 7662
- 추천과 검색
- 유튜브 추천 시스템
- 백준
- 특정 거리의 도시 찾기
- 파이썬
- 1259
- 10825
- Pypy3
- 추천 시스템
- 구조적 데이터
- google dialogflow
- 추천 시스템의 한계
- 3085
- 협업 필터링
- hannanum
- 추천시스템
- 유사도
- 1620
- 경쟁적 전염
- python
- Today
- Total
Kowal's Igloo
🔂 2. 신경망과 로지스틱회귀 본문
Binary Classification

- 목표: 고양이 사진이 입력으로 주어졌을 때, 고양이인지(1) 아닌지(0) 분류
- 사진 데이터는 빨강, 초록, 파랑 각각의 행렬에 저장됨
- 이 픽셀값들을 특성 벡터로 바꾸려면 모든 픽셀값을 입력 특성 벡터 x의 한 열로 나열
- 이 사진이 64 * 64 크기였으면 벡터 x의 전체 차원이 64 * 64 * 3 = 12,288이 됨. 세 행렬의 모든 원소를 포함하고 있기 때문.
- n: 입력 벡터의 차원
- 입력된 사진을 나타내는 특성 벡터 x를 가지고, 그에 대한 레이블 y가 1 아니면 0인지 예측 다시 말해 고양이 사진인지 아닌지를 예측할 수 있는 분류기를 학습하는 것
Notation

- 하나의 훈련 샘플 쌍

- x는 n_x차원 상의 특성 벡터(n은 입력 벡터의 차원. n_x = n), y는 0 또는 1

- m개의 훈련 샘플
- 훈련 세트: 첫 번째 훈련 샘플의 입력과 출력부터 마지막 훈련 샘플까지
- m_train: 훈련 세트 / m_test: 테스트 세트

행렬 X 정의
- x^(1)은 이 행렬의 첫 열로 놓고 x^(2)는 두 번째 열로 x^(m)까지 m 번째 열로 놓으면 행렬 X가 완성
- m이 훈련 샘플의 개수일 때, X는 m개의 열과 n_x개의 행들로 이루어져 있음. n_x × m 행렬
- 다른 강좌에서는 훈련 세트들을 X의 열 대신 행들로 놓았을 수 있음. (x^(1)의 전치부터 x^(m)의 전치까지) 하지만 왼쪽의 방법으로 신경망을 구현하는 게 훨씬 쉬움.
- 파이썬 명령인 X.shape로 행렬의 차원을 알 수 있음 → (n_x, m) 출력 n_x × m 행렬인 것을 뜻함
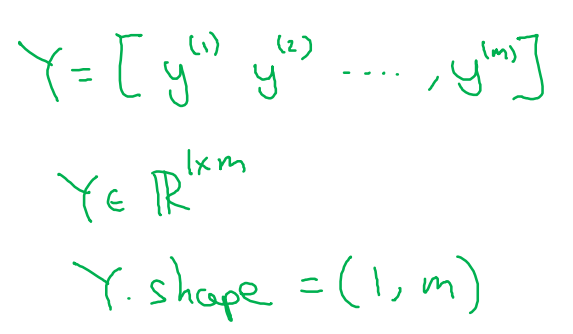
출력될 레이블 Y
- y의 값들은 열로 놓는 것이 편리
- Y는 y^(1) y^(2)부터 y^(m)으로 이루어진 1 x m 행렬
- 파이썬 Y.shape → Y의 차원 (1, m)
로지스틱 회귀 Logistic Regression
- 이 학습 알고리즘은 지도 학습 문제에서 출력될 레이블 y가 0이나 1일 경우, 즉 이진 분류 문제들에서 쓰임
- 고양이 사진인지 아닌지 구분하고 싶을 때, y의 예측값을 출력
- 여기서 y의 예측값은 입력 특성 x가 주어졌을 때 y가 1일 확률

- x는 n_x 차원 상의 벡터, 파라미터 w와 b는 각각 n_x 차원 상의 벡터와 실수
- x, w, b가 주어졌을 때, 어떻게 y의 예측값 출력?
- 선형 회귀(Linear Regression)처럼 y = wTx + b? → y는 항상 0과 1 사이인데, w의 전치 × x + b는 1보다 훨씬 크거나 음수일 수도 있음
→ 그래서 로지스틱 회귀에서는 y의 예측값에 시그모이드 함수를 적용함
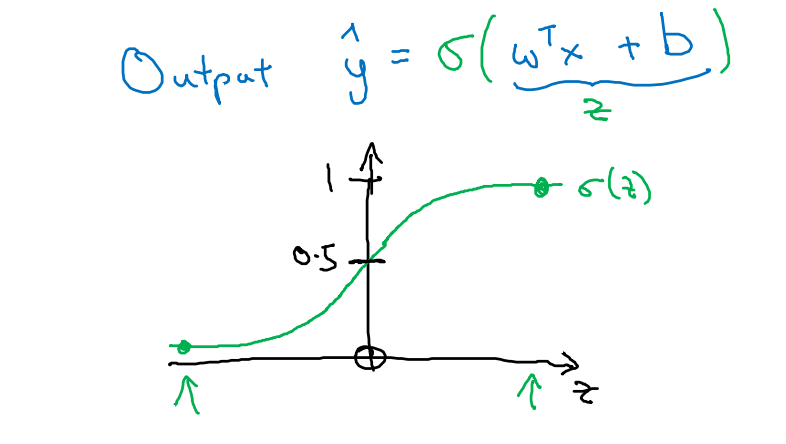
- z는 w의 전치 × x + b의 값
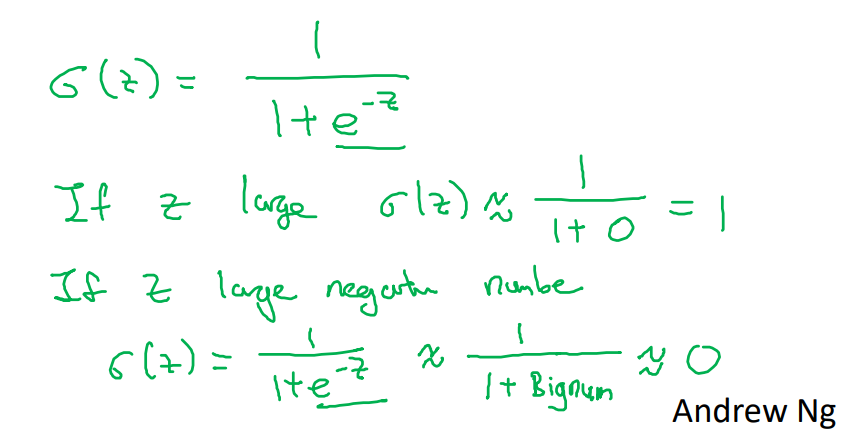
- 시그모이드 공식
- 만약 z가 매우 크면 1에 수렴, 매우 작으면 0에 수렴
- y가 1일 확률을 잘 예측하도록 파라미터 w와 b를 학습해야 함.
로지스틱 회귀의 비용함수
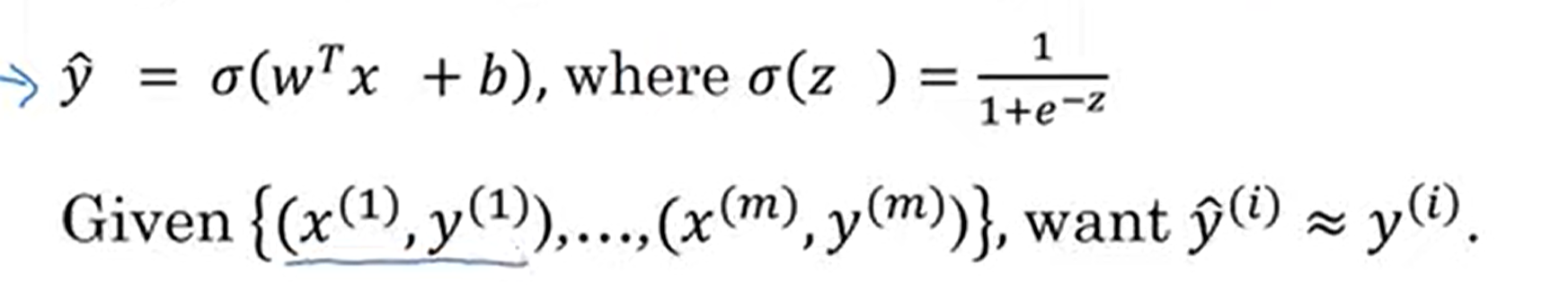
- 매개변수 w와 b를 학습하려면 비용함수를 정의해야 함.
- 위첨자 (i): x이든 y이든 z이든 i번째 훈련 샘플에 관한 데이터
- y의 예측값은 w의 전치 × x + b의 시그모이드
- w와 b는 매개변수
- 주어진 m개의 훈련 샘플로 학습할 때, 훈련 세트를 바탕으로 출력한 y^(i)의 예측값이 훈련 세트에 포함된 참값 y^(i)에 가까워지도록 하는 게 목표

최적화함수는 볼록해야 좋음. 여러 개의 지역 최적값을 가지고 있으면 전체 최솟값을 찾을 수 없을 수도 있음.
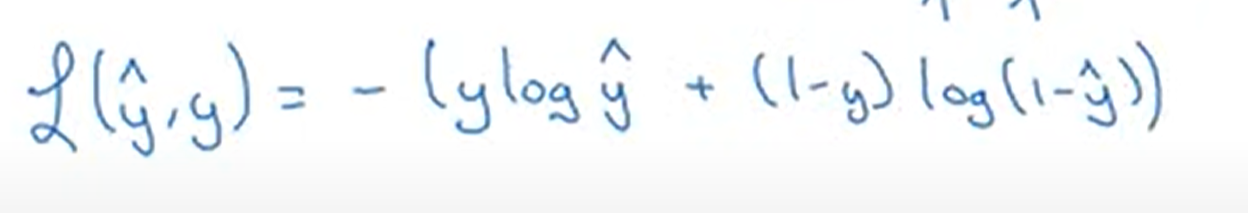
- 로지스틱 회귀에서 쓰는 오차함수
L은 손실 함수이고, y의 예측값과 y의 참값 사이에 오차가 얼마나 큰지 측정. 이 오차를 최소화하고 싶음.
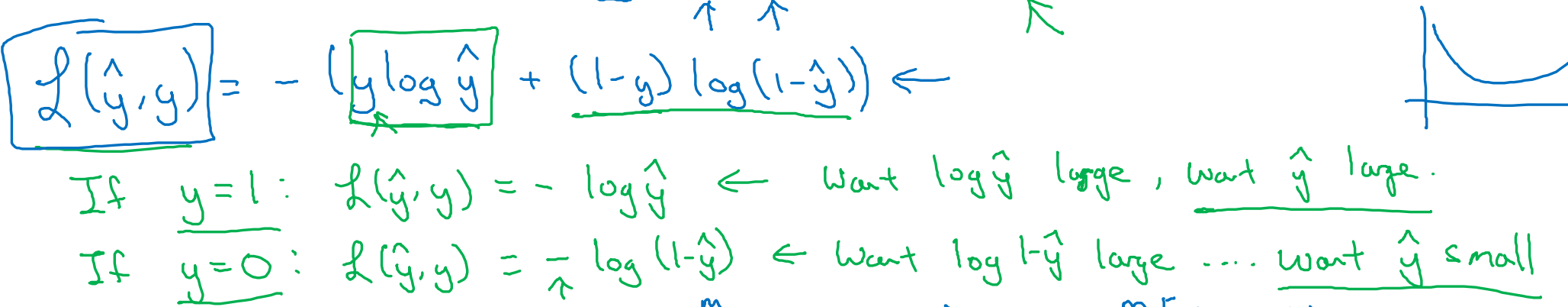
- 그렇다면 이걸 왜 쓸까?
y가 1일 때: y의 예측값이 최대한 커야 함. 그런데 시그모이드 함수의 결과값인 y의 최대값은 1임. 따라서 y가 1에 수렴하길 원함.
y가 0일 때: y의 예측값이 최대한 작아야 함. 그런데 시그모이드 함수의 결과값인 y의 최소값은 0임. 따라서 y가 0에 수렴하길 원함.
→ 손실 함수는 y의 예측값이 원하는 값에 수렴하도록 매개변수들을 조절할 것
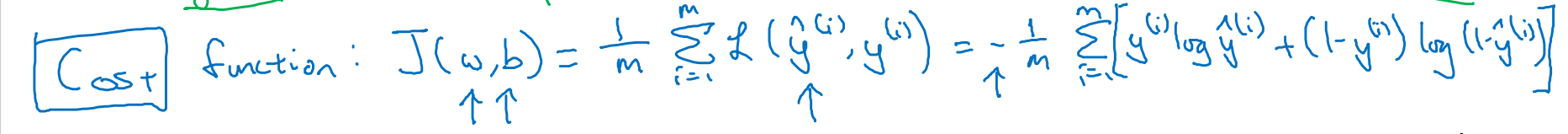
- 손실 함수(Loss/error function)는 훈련 샘플 하나에 관하여 정의
- 비용 함수(Cost function)는 훈련 세트 전체에 대해 정의, 매개변수의 비용처럼 작용함
비용 함수는 매개 변수 w와 b에 대해 손실 함수를 각각의 훈련 샘플에 적용한 값의 합들의 평균, 즉 m으로 나눈 값
→ 결과적으로 로지스틱 회귀 모델을 학습하는 것: 비용 함수 J를 최소화해주는 매개 변수들 w와 b를 찾는 것
경사 하강법 (Gradient Descent)
- 경사 하강법 알고리즘을 사용해 매개변수 w와 b를 훈련 세트에 학습시키는 방법을 배울 것

- 로지스틱 회귀 알고리즘
- 비용 함수 J : 손실 함수의 합의 평균
- 비용 함수의 역할: 매개변수 w와 b가 훈련 세트를 잘 예측하는지 측정
- w와 b의 공간. 비용 함수 J(w, b)는 가로축 w, b 위의 곡면이고 곡면의 높이는 그 점의 J(w, b) 값
- 매개변수 w와 b를 알아내기 위해서는, 비용 함수 J(w,b)를 가장 작게 만드는 w와 b를 찾아야 함.
경사 하강법 과정
- w와 b 초기화 필요, 보통 0으로 설정함. 볼록한 함수이기 때문에 어디서 초기화하더라도 같은 점에 도착
- 가장 가파른 방향으로 한 단계 내려감
- 계속 내려가며 최솟값을 찾음
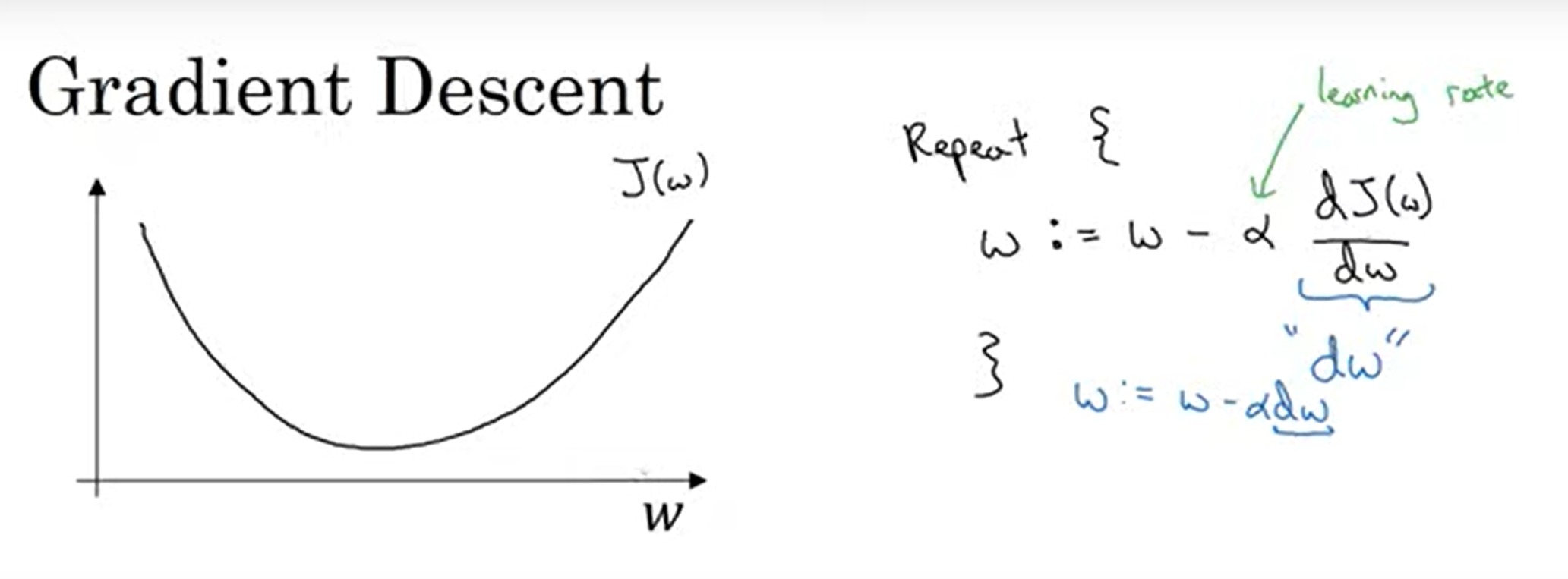
- :=는 값을 업데이트한다는 뜻
- α: learning rate
- J(w)의 미분계수를 dw라고 함. = 함수의 기울기
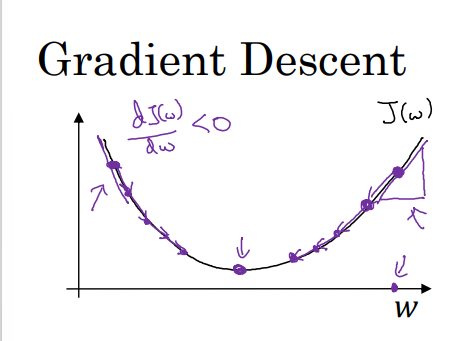
- w > 0이면 기울기 > 0, w값 감소
- w < 0이면, 기울기 < 0, w값 증가
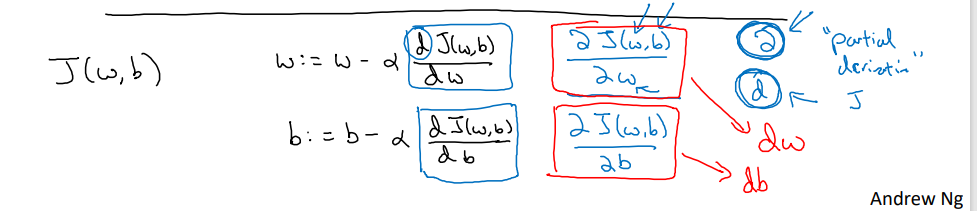
- 골뱅이같이 생긴 문자는 소문자 d를 다른 글씨체로 쓴 것
- J가 두 개 이상의 변수를 가진 함수일 때 d 대신 사용 (편미분 기호) 편미분은 여러 변수 중 하나에 대한 함수의 기울기를 구하는 것
- 코드 구현 시, w의 변화량은 dw, b의 변화량은 db로 표시함.
미분 (Derivatives)

- a를 오른쪽으로 0.001만큼 밀었을 때, f(a)는 0.003 증가함. 즉 f(a)가 증가한 정도는 a가 증가 정도보다 세 배 많음
- 도함수(derivative) = 기울기(slope) = 삼각형의 높이/밑변
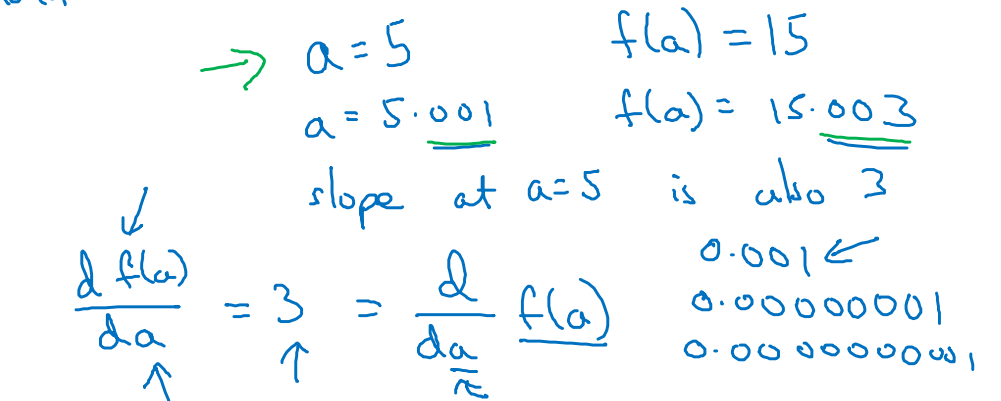
- df(a)/da = 변수 a를 아주 조금(무한소만큼) 움직였을 때 함수 f의 기울기 = 3
- 이 함수의 특성은 함수의 어느 곳이든 기울기가 3이라는 것
더 많은 미분 예제(More Derivative Examples)
- f(a) = a². 입력값에 따라 기울기가 다른 함수
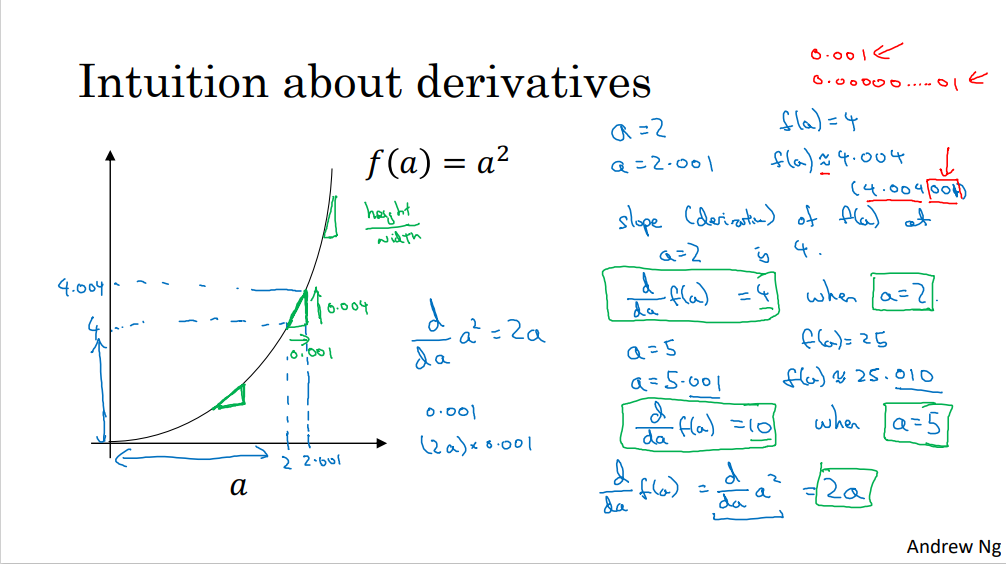
- a = 2이면, 기울기는 4
- a = 5이면, 기울기는 10
- 각 점에서 삼각형을 그려보면 높이/밑변의 비율이 다른 걸 알 수 있음.
- 아무 값 a를 아주 작은 값 0.001만큼 밀었을 때 f(a)의 값은 2a만큼 증가한다.
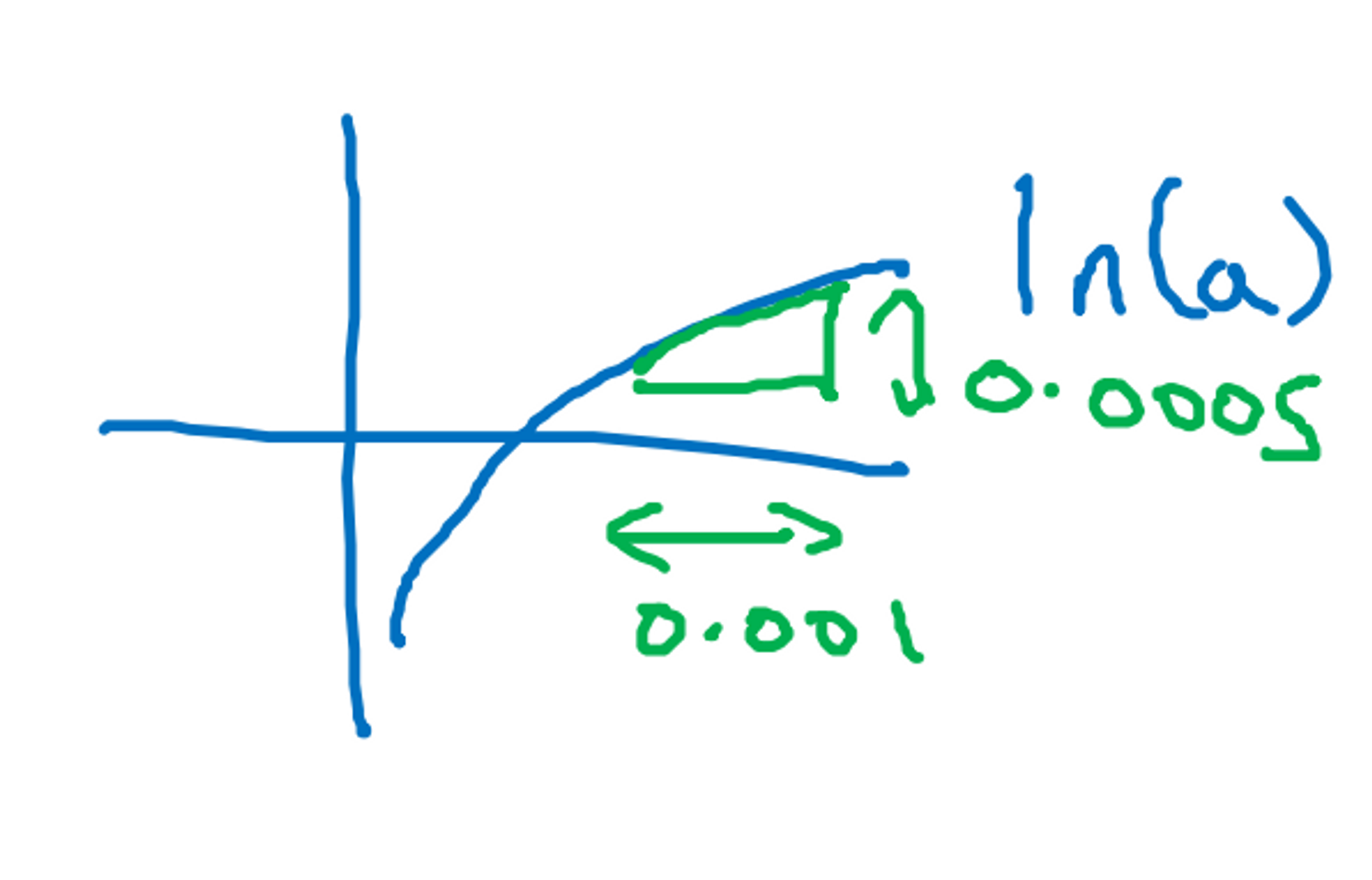
- f(a) = a³ → (d/da)·(f(a)) = 3a²
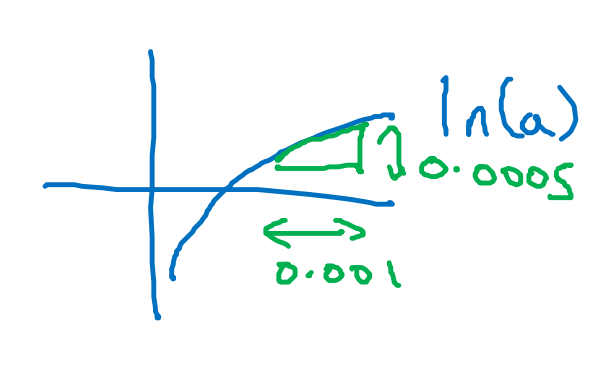
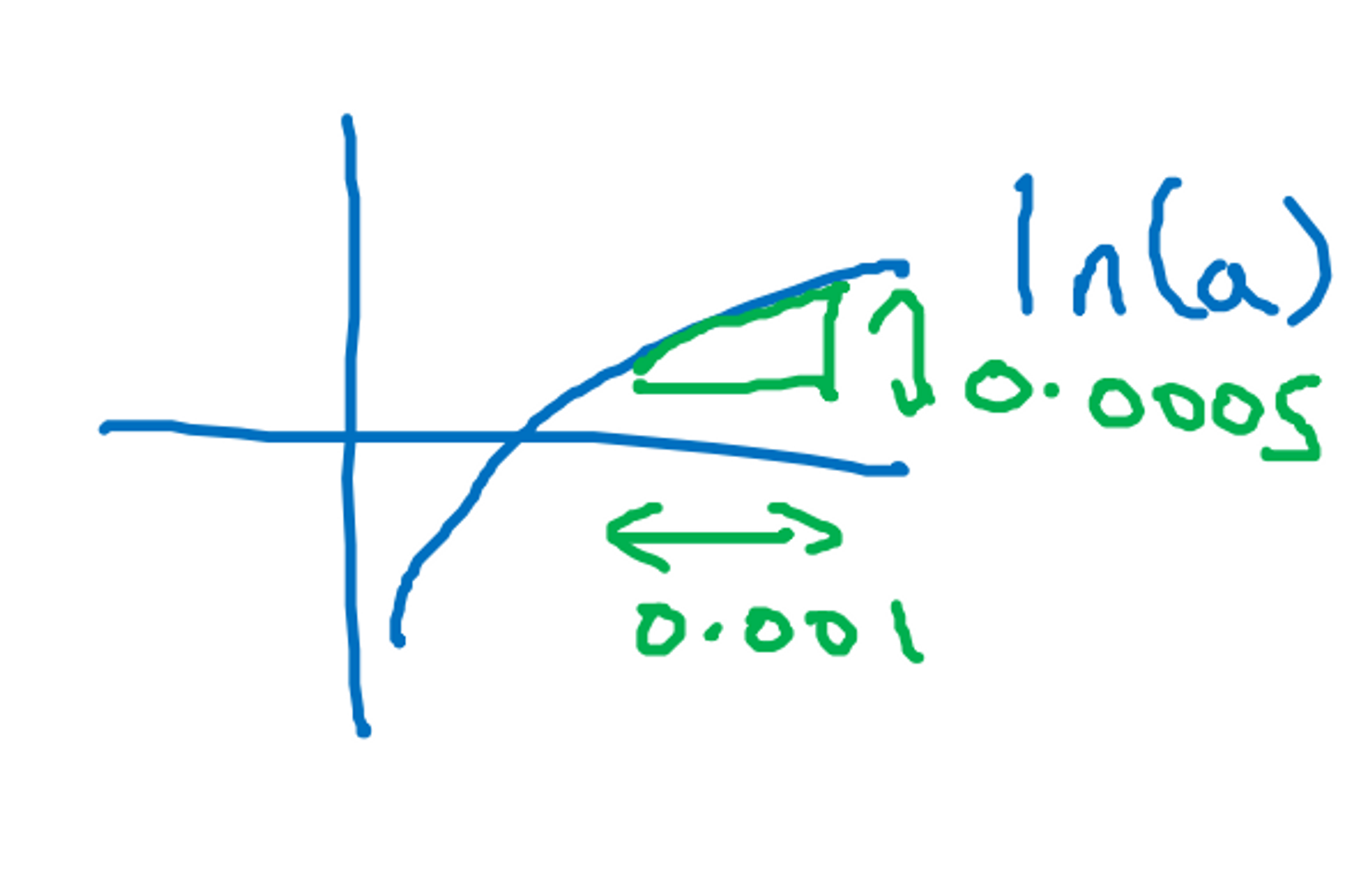
- f(a) = ln(a), (d/da)·(f(a)) = 1/a
→ 도함수는 선의 기울기
첫 예제였던 f(a) = 3a는 직선이어서 미분계수가 모든 곳에서 같았음. 하지만 뒤의 예시들은 선의 기울기가 다르기 때문에, 위치가 달라지면 도함수의 값이 달라짐.
→ 어떤 함수의 도함수를 찾아야 할 때, 미적분 관련 책이나 위키피디아를 보면 공식을 확인할 수 있음
계산 그래프 (Computation Graph)
신경망의 계산은 두 가지로 나뉨.
- forward pass or a forward propagation step
- backward pass or a backward propagation step
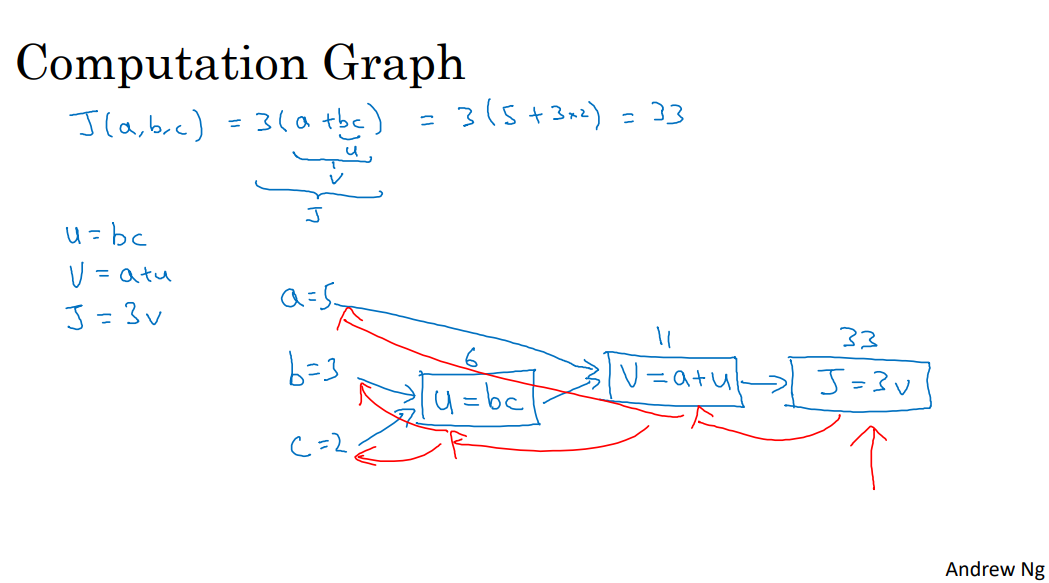
- 계산 그래프는 J와 같이 특정한 출력값 변수를 최적화하고 싶을 때 유용
- 로지스틱 회귀의 경우에 J는 최적화할 비용 함수
- J값(비용 함수) 계산: 왼쪽 → 오른쪽
- 도함수 계산: 오른쪽 → 왼쪽
계산 그래프로 미분하기 (Computing Derivatives)
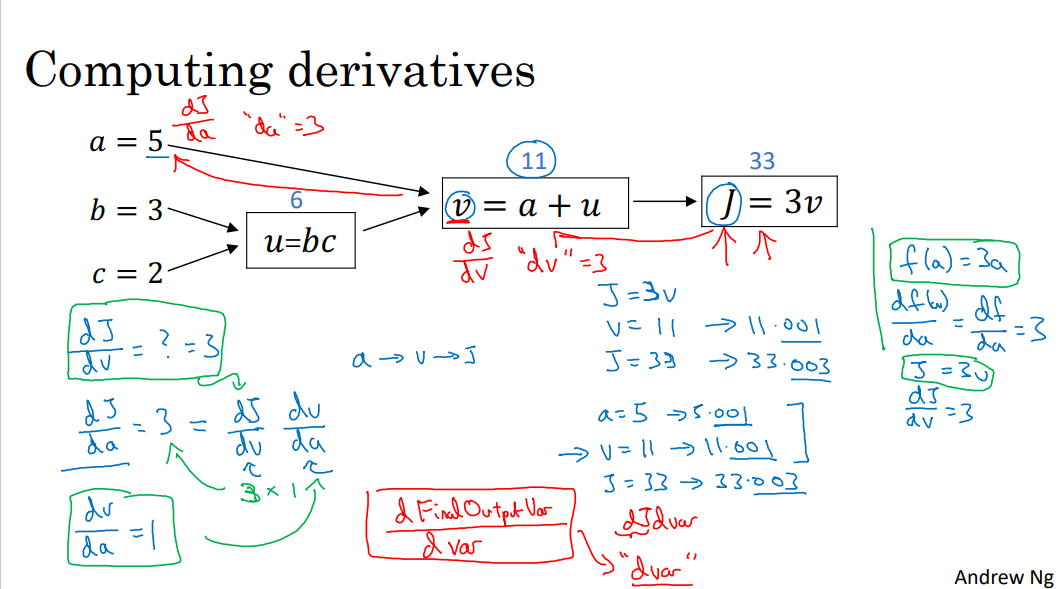
- J = 3v, dJ/dv = 3
- dJ/da는?
- 연쇄법칙
- 역방향 전파를 구현할 때, 구하고자 하는 최종 출력값이 있을텐데 아마 최적화 하려는 값일 것. 여기서 최종 출력값은 J. 계속 최종 출력값 J의 도함수를 구하고 있는 것이니까 변수 이름을 dvar라고 함. (dv, da, …)
- db = dJ/db = dJ/dv * dv/du * du/db
로지스틱 회귀의 경사하강법 (Logistic Regression Gradient Descent)
- 로지스틱 회귀 복습
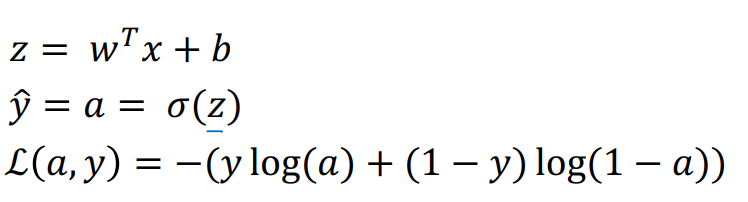
- z 정의
- y의 예측값
- 하나의 샘플에 대한 손실 함수(Loss/error function)
a: 로지스틱 회귀 출력값 (y 예측값), y = 참값
- 이걸 계산 그래프로 나타내보면
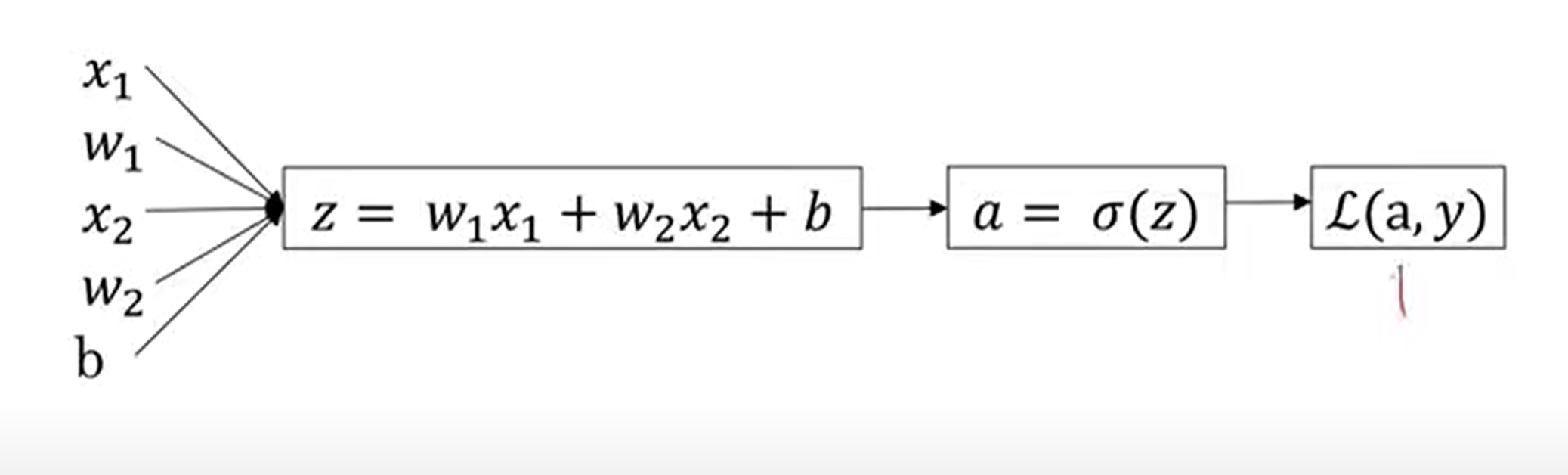
- 로지스틱 회귀의 목적

- da=−y/a+1−y/1-a
- dz = a - y
- dw1=dL/dw1=x1dz
- db=dL/db=dz
m개 훈련 샘플에 대한 경사하강법
- m개의 훈련 샘플의 cost function (1부터 m까지 더한 값의 평균값)
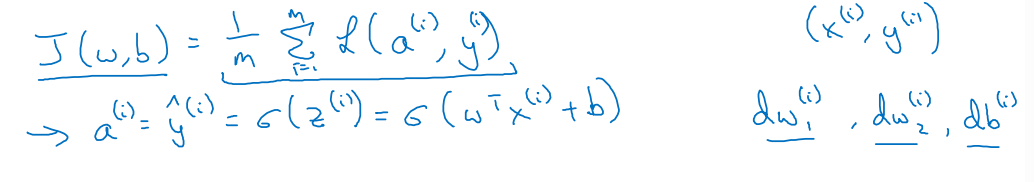
- 전체 비용 함수의 도함수도 각 손실 항 도함수의 평균값
→ 경사 하강법에 사용할 전체적인 경사를 구할 수 있음
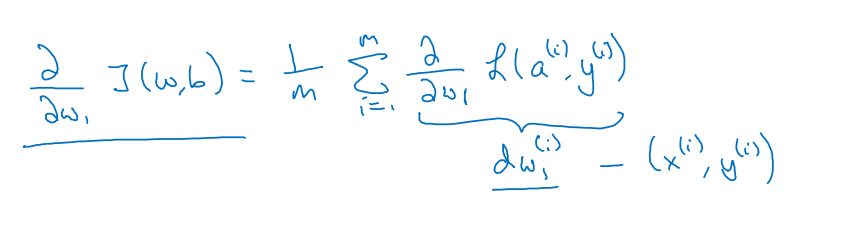
프로그래밍

- J = 0, dw_1 = 0, dw_2 = 0, db = 0으로 초기화
- 훈련 세트를 반복해 각 훈련 샘플에 대한 도함수를 계산하고 이를 더해 dw와 db를 업데이트할 것
- z^(i) = w^T·x(i) + b와 예측값 a^(i) = σ(z^(i))를 계산하고 J에 더함
- 도함수 계산 (n = 2라고 가정)
- 평균 계산을 위해 J, dw, db를 모두 m으로 나눔
- dw는 w에 대한 전체 비용 함수의 도함수
- w_1 := w_1 - (학습률 α) dw_1
→ 이 과정은 모두 경사 하강법 한 단계에 사용됨. 여러 번 진행하려면 반복 필요.
두 가지 단점
- for 문을 두 개 만들어야 함
첫 번째 for 문: m개의 훈련 샘플 반복 / 두 번째 for 문은 dw를 계산하며 특성(n)을 반복
- 딥러닝 알고리즘을 구현할 때 이런 명시적인 for 문은 알고리즘을 비효율적으로 만듦. for문이 없어야 더 큰 데이터 집합 처리 가능
→ 벡터화로 명시적인 for문 삭제 가능
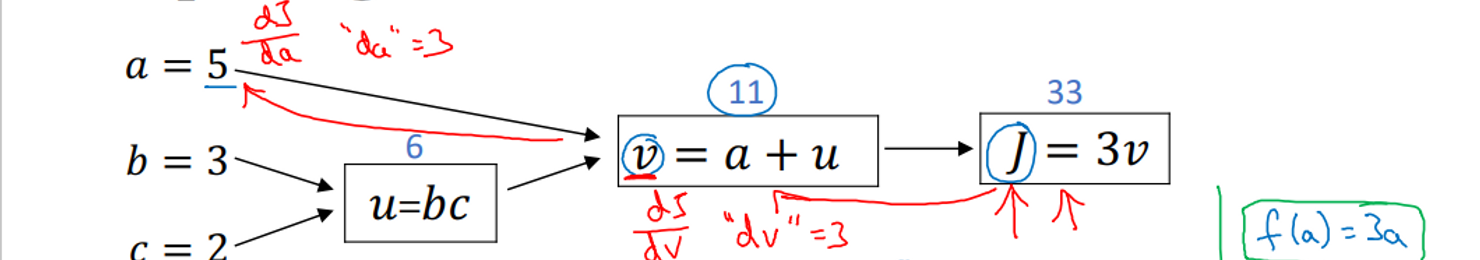

'AI' 카테고리의 다른 글
| 🖍️ [딥러닝 2단계] 1. 머신러닝 어플리케이션 설정하기 (0) | 2025.01.07 |
|---|---|
| 📑 4. 얕은 신경망 네트워크 (2) | 2025.01.07 |
| 🔢 3. 파이썬과 벡터화 (2) | 2025.01.07 |
| 추천 시스템: 코사인 유사도를 활용한 키워드 기반 추천 알고리즘 (0) | 2023.11.24 |
| 신경망과 딥러닝 (2) | 2023.09.19 |




