| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 넷플릭스 추천 시스템
- 10825
- 추천 시스템
- 14620
- 추천시스템
- 앤드류 응
- 추천과 검색
- 파이썬
- hannanum
- 18352
- python
- 백준
- 경쟁적 전염
- 협업 필터링
- 구조적 데이터
- 1259
- 7662
- 유튜브 추천 시스템
- 특정 거리의 도시 찾기
- 추천 시스템의 한계
- 1620
- 문자열반전
- 유사도
- Pypy3
- google dialogflow
- 3085
- 알고리즘
- 18405
- 컨텐츠 기반 필터링
- 7785
- Today
- Total
Kowal's Igloo
📈 [딥러닝 2단계] 2. 신경망 네트워크의 정규화 본문
정규화 (Regularization)
모델 가공 - 훈련, 테스트에 모두 적용됨
Overfitting에서 가장 처음에 시도해야 할 것은 정규화이다. 훈련 데이터를 늘리는 것도 방법이지만, 비용이 많이 소비된다.
Logistic Regression 정규화
- L2 Regularization


정규화는 weight 값에 패널티를 적용하는 방식으로 작동한다. L2 정규화는 w^2의 norm에 람다를 곱한 값을 전체 비용 함수에 더한다. w^2의 norm은 j = 1부터 nx까지 wj^2의 값을 더한 값으로, wTw와 같다. b 대신 w만 정규화하는 이유는, 매개변수 w의 수가 훨씬 많아 복잡한 벡터로 표현되기 때문이다.
- L1 Regularization (L2보다 훨씬 덜 일반적)

L1 정규화는 |w|의 합을 람다에 곱한다. L1 정규화를 사용하면 모델이 희소해지는데, 이는 벡터 안에 0 요소가 많아져 모델이 압축된다는 뜻이다. 모델을 압축하는 목표가 있지 않다면 이 정규화는 사용하지 않는다.
- Lambda

개발 세트, 교차검증 세트에 주로 활용한다. 다양한 값을 시도하면서 training 세트에 잘 맞으면서도 overfitting되지 않는 값을 찾는다. 즉, Lambda는 인간이 조작하는 하이퍼파라미터이다.
파이썬에서 이미 lambda라는 명령어가 있기 때문에 lambd로 사용한다.
Neural Network 정규화

비용함수에 λ를 2m으로 나눈 값 * w norm^2의 합을 더한다. w norm^2은 i(1 ~ n^[l-1]), j(1 ~n^[l]에 해당하는 각각 행렬의 원소를 제곱하는 값을 모두 더한 것이다. w는 (n^[l], n^[l-1]) 차원의 행렬이기 때문에 i, j는 해당 층 l-1과 l의 은닉 유닛의 개수를 나타낸다. 행렬의 원소 제곱의 합이기 때문에, 이 norm은 L2 norm 대신 프로베니우스 norm이라고 한다.
Gradient Descent

기존 dw 계산식에 정규화 항을 더한다.
Weight Decay

위 식을 풀어서 작성하면 그림과 같이 되는데, w를 업데이트할 때마다 값이 더 작아진다는 것을 알 수 있다. 항상 w에 1보다 작은 값을 곱해주기 때문이다. 이러한 이유로 L2 정규화의 다른 이름을 weight decay라고 한다.
단점
매개변수 λ에 많은 값을 대입하며 계산해야 한다.
정규화가 과대적합을 줄이는 이유
L2 norm(프로베니우스 norm)이 어떻게 과대적합을 줄일 수 있을까?

정규화는 λ를 증가시켜 weight를 0에 가깝게 만들고, 이는 은닉 유닛을 0에 가까운 값으로 설정한다. 따라서 더 작고 간단한 신경망이 된다.

tanh를 사용할 때, z가 0에 가까운 매개변수를 갖는다면 tanh 함수의 선형 영역을 사용하게 된다. w가 작은 값을 가지면 g(z)는 거의 직선의 함수가 된다. 각 층이 선형이면 전체 네트워크도 선형이 되기 때문에, 신경망 자체가 더 간단해진다. 따라서, 과대적합이 줄어든다.
드롭아웃 정규화 (Dropout Regularization)
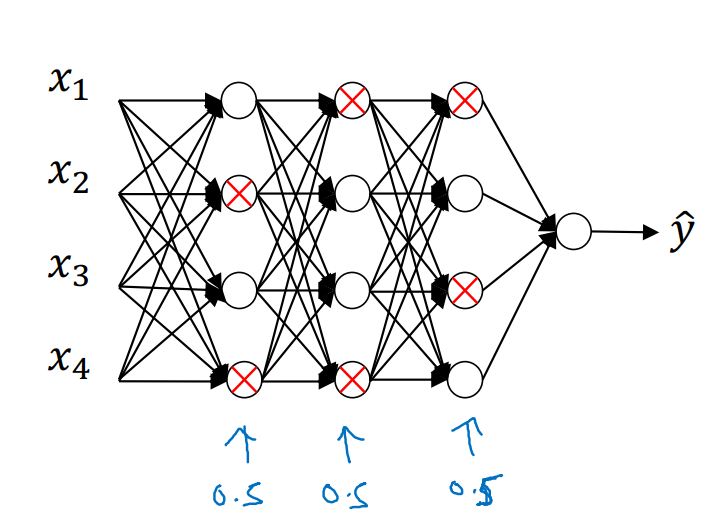
드롭아웃은 신경망의 각 층에 대해 노드가 삭제될 확률을 설정하는 것이다. 즉, 은닉 노드를 무작위로 삭제하여 네트워크를 더 작게 만든다.
역 드롭아웃 (Inverted Dropout)

keep_prob은 해당 은닉 유닛을 유지할 확률이다. 여기에서는 0.8로 설정하였으므로, 유닛이 삭제될 확률이 0.2라는 것을 뜻한다.
과정은 아래와 같다.
- a3와 같은 모양인 d3 드롭아웃 벡터 설정
- 각각의 유닛이 keep_prob보다 작은지 비교하고, 작으면 d3를 0으로, 크면 1로 설정
- a3를 a3와 d3를 곱한 값으로 업데이트
- a3의 남은 값을 원래대로 설정하기 위해 keep_prob으로 나누기
경사 하강법에서 하나의 반복마다 0이 되는 은닉 유닛은 무작위로 달라져야 한다.
테스트
테스트에서는 드롭아웃을 사용하지 않는다. 결과가 무작위로 나오면 소용이 없기 때문이다. 드롭아웃을 추가하지 않아도 활성화값의 크기는 변하지 않기 때문에, 테스트 시 스케일링 매개변수를 추가하지 않아도 된다.

드롭아웃의 이해
드롭아웃은 무작위로 신경망의 유닛을 삭제하는 기법인데, 어떻게 이 방법이 과대적합에 효과가 있을까?

드롭아웃을 통해 입력이 무작위로 삭제되므로, 신경망은 하나의 특성에 의존할 수 없다. 그 특성이나 입력이 무작위로 바뀔 수 있기 때문이다. 즉, 특정 입력에 큰 가중치를 부여하는 걸 피하고 가중치를 분산시킴으로써 가중치 norm의 제곱이 줄어든다. 이는 L2 정규화와 비슷한 효과를 낸다. (L2 정규화가 다른 가중치에 적용된다는 것과 서로 다른 크기의 입력에 더 잘 적응한다는 것만 다른 부분)
Keep_prob 다양화
구현 시, 층마다 keep_prob을 변화시키는 것도 가능하다. 과대적합 가능성이 높은(유닛 수가 많아 매개변수의 수가 많은) 층에 대해 keep_prob을 작게 설정한다. 과대적합의 우려가 없는 층은 keep_prob을 1로 설정해도 된다. 입력층에서는 보통 1에 가까운 keep_prob을 사용한다.
이렇게 keep_prob을 다양화하는 것의 단점은 교차검증을 위해 더 많은 하이퍼파라미터가 생긴다는 것이다.
컴퓨터 비전에서는 데이터가 부족하기 때문에 드롭아웃을 매우 자주 사용한다.
드롭아웃의 단점
드롭아웃의 큰 단점은 모든 반복에서 잘 정의된 비용함수가 하강하는지 확인하는게 어려워진다는 것이다. 따라서 우선 드롭아웃을 사용하지 않고, 비용함수가 단조감소인지 확인한 후에 사용해야 한다.
다른 정규화 방법들
Data Augmentation

이미지를 뒤집거나, 회전시키거나, 확대, 왜곡하는 등 가짜 훈련 샘플을 추가한다. 새로운 고양이 샘플보다 많은 정보를 추가하지는 않지만, 적은 비용으로 데이터를 얻을 수 있는 방법이다. 이 방법으로 정규화해 과대적합을 방지할 수 있다.
조기 종료 (Early Stopping)

조기 종료는 신경망이 개발 세트의 오차 저점 부근, 즉 가장 잘 작동하는 점일때 훈련을 종료한다. 훈련이 조금 진행되었을 때, 매개변수 w는 0에 가까운 값을 가진다. 반복을 계속하며 w의 값이 커지는데, w가 중간 정도의 값을 가졌을 때 훈련을 중지한다.
경사 하강법 과정을 한 번만 실행해도 작은 w, 중간 w, 큰 w의 값을 모두 얻을 수 있다는 점이 장점이다.
단점
훈련 시 우리의 목표는 두 가지이다. 비용 함수를 최적화 시키는 일, 그리고 과대적합을 방지하는 일이다. 이 두 작업은 독립적이기 때문에 두 가지 다른 방법으로 접근해야 하지만, 조기 종료는 하나의 방법으로 두 문제를 모두 해결하려고 한다. 즉, 비용함수 J를 줄이는 일과 과대적합을 줄이는 일을 한꺼번에 수행하게 되어 문제를 해결하지 못할 수 있다.
Q & A
- normalization: 분산을 줄여주는 방법
- 적은 데이터를 사용할 때는 드롭아웃이 좋은 선택이 아님
부스트코스에서 앤드류 응 교수님의 강의를 듣고 정리한 내용입니다.
'AI' 카테고리의 다른 글
| 🍎 [딥러닝 2단계] 5. 하이퍼파라미터 튜닝 (0) | 2025.01.07 |
|---|---|
| 🖌️ [딥러닝 2단계] 3. 최적화 문제 설정 (1) | 2025.01.07 |
| 🖍️ [딥러닝 2단계] 1. 머신러닝 어플리케이션 설정하기 (0) | 2025.01.07 |
| 📑 4. 얕은 신경망 네트워크 (2) | 2025.01.07 |
| 🔢 3. 파이썬과 벡터화 (2) | 2025.01.07 |




